중심극한정리(Central Limit Theorem) 이해하자
중심극한정리란 “모집단의 분포와 상관없이 표본의 크기가 충분히 커지면 표본평균의 분포가 정규분포에 가까워진다.” 이다. 이때 충분히 큰 표본은 30으로 보고 있다.
(아래 그림은 모집단이 마치 정규분포인 것 처럼 그렸으나 실제로는 어떠힌 분포인지는 상관이 없다.)
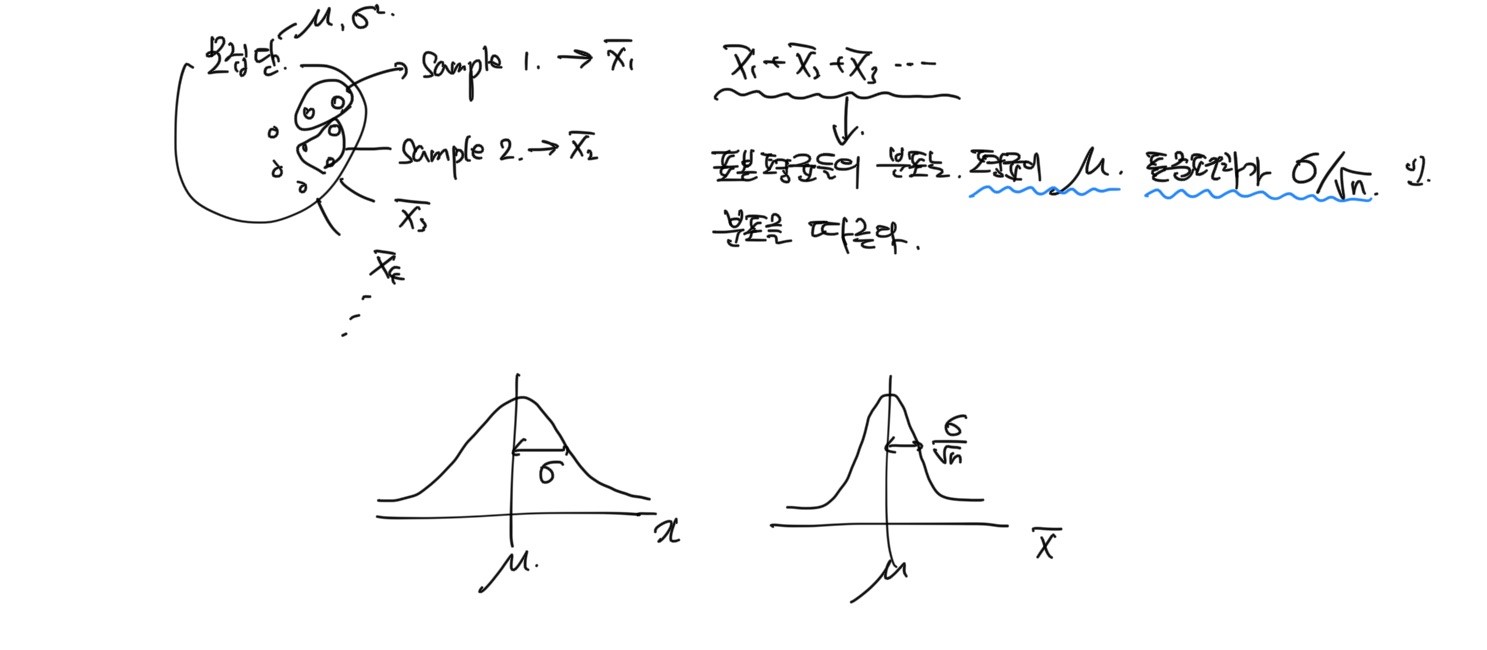
여기서 표본수(n)는 표본평균들의 개 수가 아닌 하나의 표본평균을 산출하기 위해 추출된 샘플 수를 의미한다. 그리고 표본추출을 할 때는 기본적으로 복원추출을 전제로 한다.
중심극한정리가 중요한 이유은 추리통계에서 이론적 근거를 제시하고 있기 때문이다. 모집단이 어떤 분포를 가지고 있던지 간에, 표본의 크기가 충분히 크면 표본평균들의 분포가 모집단의 모수를 기반으로한 정규분포를 이룬다는 것이다. 이를 바탕으로 수집한 표본의 평균이 일어날 확률값을 계산할 수가 있게 된다.
다시 정리하면, 중심극한정리는 표본 평균들이 이루는 표본 분포와 모집 단간의 관계를 증명함으로써, 수집한 표본의 통계량을 이용해 모집단의 모수를 추정할 수 있는 수학적 근거를 마련해주게 된다.
