Gradient Descent 이해하기
Idea
딥러닝에서 문제를 푼다는 것은 아주 복잡한 고차원의 함수(Objective fuction or Cost fuction)에 대해서 Minimize 하는 것이다. 최소점으로 이동하기 위해서는 미분이라는 과정을 통해서 현재 위치한 지점에서의 기울기를 구하고 기울기의 반대방향으로 조금씩 이동해가며 극소점을 찾아게 된다.
Learning rate
이때 이동할 때, 얼마나 이동할 것인지 step을 정의해야 하는데, step을 learning rate로 표기한다. Learning rate 라는 값을 크게 주면 극소점을 향해 빠르게 수렴해가겠지만, 극소점 근처에 다다랐을 때는 오히려 큰 learning rate 때문에 극소점으로 수렴을 하지 못할 수도 있다. 반대로 learning rate가 너무 작으면 극소점으로의 수렴자체가 너무 오래 걸릴 수 있다. 그래서 이러한 learning rate도 하나의 모델을 Optimization을 위한 하나의 하이퍼파리미터가 된다.
Initial point
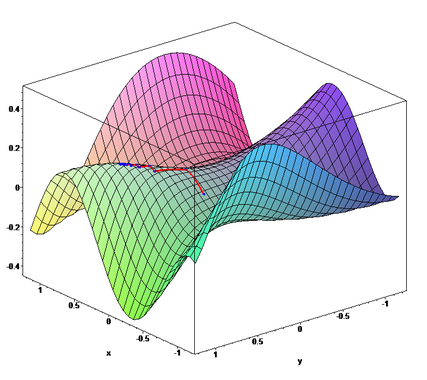
위에서 살펴본 경사하강법에서 또 한가지 중요한 것은 Initial point이다. 아래 그림을 참고해보자.
딥러닝에서의 Cost fuction은 대단히 복잡한 함수가 될 것인데, 이를 기하학적으로 그려보면 Manifold가 된다. 그러면 초기값을 어느 위치에서 시작하느냐에 따라서 Global Optimim에 수렴하지 못하고 Local optimum에 머무를 수 있다.
Stochastic Gradisen Descent
그렇다면 확률적 경사 하강법은 무엇일까? 거의 대부분 딥러닝은 확률적 경사하강법이라고 하는 알고리즘으로 optimization이 진행된다. 우리가 딥러닝에서 일반화가 잘 되기 위해서는 학습 데이터 양이 많아야 한다. 그런데 일반적인 경사 하강법은 데이터 양이 많아지면 많아질 수록 그 연산에 대한 비용이 커진다는 문제점이 있다. 결국 확률적 경사 하강법이 등장하게 되는데, 기울기가 하나의 기대값인 것이다. 학습데이터 보다 훨씬 더 적은 수의 샘플 데이터를 이용해서 기울기를 근사적으로 추정하는 방식인 것이다. 여기서의 샘플 수가 하나의 미니배치 단위 이다.
학습데이터가 늘어난다 하더라도 미니배치의 수는 고정하는 경우가 많기 때문에 계산량이 증가하지 않는다. 물론 수렴을 위한 갱신 횟수는 학습 데이터 양에 비례하긴 하지만, 만약 데이터 양이 무한대로 증가한다면 SGD가 학습 데이터 모두를 표본으로 추출하기 전에 모델은 test error가 best인 지점에 도달한다.